PID控制器算法原理讲解从入门到精通详细教程工控PID算法参数整定串级PID算法讲解

2018-2-19 21:09:05

仅

供

学

习

参

考

PID算法讲解与参数整定经验分享文档v1.0writed by 朱子文，如果您有任何问题或者建议，请邮件联1304546267@qq.com， 谢谢您的支持!

一、PID控制器的简介

目前工业自动化水平已经成为衡量各行各业现代化水平的一个重要标志。同时控制理论的发展也经历了古典控制理论-现代控制理论-智能控制理论三个阶段。自动控制系统可分为开环控制系统和闭环控制系统。整个控制系统包括：控制器（CPU）、传感器、输入输出接口、执行机构等部分组成。

工业生产过程中，对于生产装置的温度、压力、流量、液位等工艺变量常常要求维持在恒定的数值上，或按一定的规律变化，以满足生产工艺的要求。PID控制器是根据PID控制原理对整个控制系统进行偏差调节，从而使被控变量的实际值与工艺要求的给定值一致。

而PID的是英文Proportion（比例）-Integral（积分）-Differential（微分）的英文首字母，其中文名称是：比例-积分-微分控制器。

PID 可谓是相当经典的一种控制策略，据我所知目前涉及到自动控制的很多场景都在使用 PID 控制器。（也有其他高级控制器，比如自抗扰ADRC控制算法）PID控制器的问世至今已有70年历史，它以结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。而当被控对象的结构和参数不能完全掌握，或者说得不到精确的数学模型的时候，控制理论的其他技术将难以采用，系统控制器的结构和参数必须依靠经验和现场调试来确定时，PID控制技术可能是比较理想的控制方案。也就是说当我们不了解一个系统和被控制对象，或者不能通过有效的手段来获得系统参数时，最适用使用PID控制技术。PID控制技术根据实际需要还可以分为P控制PI控制PD控制以及其他的优化变形。PID控制器其实就是根据系统的偏差，利用比例环节、积分环节、微分环节计算出控制量进行控制的。

PID控制器的算法实现不是难点，难点是 PID参数的整定调试。一般工程人员采用的都是经验法调试，如果经验不足则可能很难找到合适的参数。本文我们将使用微型四轴以及自平衡小车为PID调试载体，带大家了解PID的参数整定过程。

二、PID相关名词解释

首先给大家解释一下相关的名词，我们下面会用到这些东西。

1.PID

PID的是英文Proportion（比例）-Integral（积分）-Differential（微分）的英文首字母，其中文名称是：比例-积分-微分控制器。

2.被控对象

在本篇文章中的控制对象就是微型四轴和我们的自平衡小车。我们将在第5部分和第六部分带着大家整定微型四轴和自平衡小车的PID参数。

3.开环系统

开环系统指的是被控对象的输出（被控制量）对控制器的输出没有影响， 在这种控制系统中，没有形成闭环回路。本次输出量没有进行反馈，不影响下次输出量。

4.闭环系统

闭环系统的特点是系统被控对象的输出（被控制量），会通过反馈通道返送回来影响控制器的输出，形成一个或者多个闭环系统（单环就是一个闭环，串级一般就是指两个闭环。而我们的微型四轴和自平衡小车使用的均是串级双环PID，其内环为角速度环，其外环为角度环）。闭环控制系统有正反馈和负反馈，如果反馈回来的信号数值符号与给定的信号相反，则称为负反馈。如果极性相同就称为正反馈，一般的闭环控制系统使用的都是负反馈。闭环控制系统用处特别特别的多，其不仅仅局限在技术领域，非技术领域比如一个团队的管理，一个公司的组织运营等等都离不开闭环系统。

5.阶跃信号

如下图，在t0时刻突然给一个信号，让其稳定在另一个值，这就是阶跃信号。信号从0变到1然后稳定为1，我们就称这个信号为单位阶跃信号。而当这个阶跃信号输入到一个系统中，我们会得到相应的输出而这个输出我们就称之为阶跃响应。

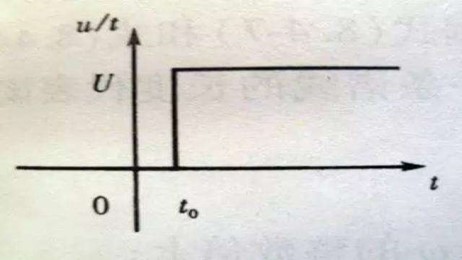
图2.1 阶跃信号

6.期望值

期望值又称为给定值，或者说是目标值。在我们的四轴中期望值就是遥控器给定的值，我们四轴中遥控器的给定值就是目标角度和目标角速度。我们自平衡小车中的给定值也是给定的目标角度和目标角速度。与其对应的就是我们的传感器测量得出的实际值。

7.偏差

上述说到的目标值减去实际值就是我们的偏差值。

8.系统中的稳态误差

&emsp&emsp系统的稳态误差，我们平常又称之为静差。稳态误差指的是系统的响应进入问题后，系统的期望输出与实际输出之差。比如说我们的期望输出是1，但是输入信号经过了系统之后稳定下来的输出是0.9左右，这里的0.9就是实际值，而1就是期望的目标值。图2.2中，这三条响应曲线稳定后的输出均没有达到期望值，图上从5s之后的，期望值减去实际值就是系统的稳态误差又称静差。

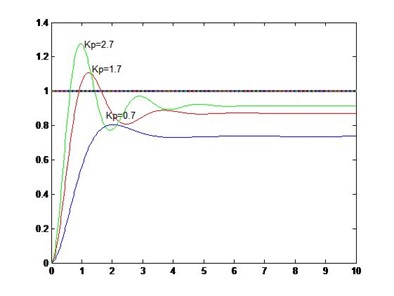
图2.2 稳态误差示意图

9.控制系统的性能

&emsp&emsp控制系统的性能可以用稳、准、快三个字来描述。稳指的是系统的稳定性，一个系统要能正常工作首要条件就是必须是稳定的。从阶跃响应来看应该是收敛的。准指的是系统的准确性，控制系统的精确度，通常我们使用稳态误差来描述，稳态误差越小其精确度越高也就是我们说的比较准确。快指的是控制系统响应的快速性，通常用上升时间来定量描述，下面这个图3种参数下的系统性能。

我们在进行PID参数整定的目的其实就是为了调节系统的稳、准、快这三个特性。

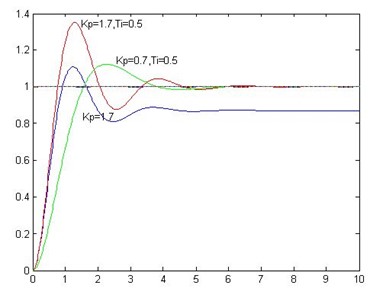
图2.3不同参数下的系统性能

红线：

    从图上，我们可以看出红线的超调比较大也就是稳定性最差，但是响应速度最快，稳态误差也很小。所以总结一下就是红线稳定性比较差，快速性很好，稳定性也很好。

紫线：

    快速性还不错，就是稳态误差很大说明其准确性不好，其超调不大说明稳定性还不错。

绿线：

    快速性最差，稳定性比较好，准确性也比较好。

10.上升时间

这里我们直接认为是 从一开始0% 到第一次达到目标值的时间100%。

三、PID的理论基础

连续-时间PID控制系统如图3-1所示。图中D(s)为控制器，在PID控制系统中，D(s)完成PID控制规律，称之为PID控制器。PID控制器是一种线性控制器，PID控制器是偏差的时间函数。

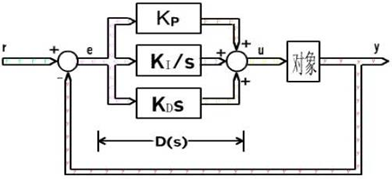
图3.1连续-时间PID控制系统

图3.1中的比例（Proportion）、积分（Integrate）、微分（Differentiation）的线性组合，构成控制量u(t),称为比例-积分-微分控制，简称PID控制。实际应用中，可以根据受控对象的特性和控制的性能要求，灵活的采用不同的控制组合。比如：

比例（P）控制器

    u(t) = Kp e(t)        (公式-1)

比例+积分（PI）控制器

比例+积分+微分（PID）控制器

当然我们平常控制电机的时候也经常使用PD控制器，这里就不给大家列公式了。

    上述公式是连续时间的函数，而我们的单片机运行程序实际上都是离散化的。我们在微型四轴和自平衡小车中调用PID函数调用周期就是2ms调用一次，也就是2ms离散化采样运算。

四、数字PID算法

在数字计算机直接数字控制中，PID控制器是通过计算机或者单片机实现的。计算机直接数字控制系统大多数都是采样-数据控制系统。进入计算机的连续-时间信号，必须经过采样和量化处理后，编程数质量，才能进入计算机的存储器和寄存器，而在数字计算机中的计算和处理，不论是积分还是微分，智能用数值计算去逼近。

在数字计算机中，PID控制规律的实现，也必须用数值逼近的方法。当采样周期相当短的时候，可以用求和代替积分，用差商代替微分，使PID算法离散化，将描述连续-时间PID算法的微分方程，变为描述离散-时间PID算法的差分方程。

A、位置式PID控制算法

图4.1位置式PID控制算法的简化示意图

上式中我们使用替换法，用矩形积分时有：

    如下图4.2所示，上式中就是矩形面积之和，得到的值近似于下图所示图形的面积。同时我们能知道只要Ts足够小，那么我们得到的近似值就越精确这就是积分的思想。

    我们知道，微分实际上就是斜率，用差分代替微分有：

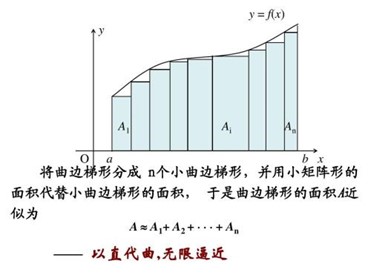
图 4.2 矩形积分示意图

将上述积分和微分的代换公式代入PID控制器的全公式有：

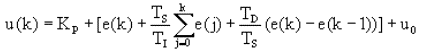
图4.3离散化PID公式1

或者写成如下形式：

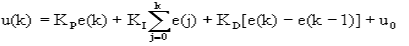
图4.4离散化PID公式2

式中u0—控制系统的控制量基准值，既k0时刻的控制量

u(k)    —— 第k时刻的控制量

Kp    —— 比例系数

Ki    —— 积分系数

Kd    —— 微分系数

Ts    —— 采样周期

    上式中是数字位置式PID形式，称为全量算法。算法中为了积分求和，我们需要在程序中设置一个变量将系统过去的所有偏差都加起来。这种控制算法得出的控制量是全量输出u(k),是控制量的绝对数值。在控制系统中，这种控制量确定了执行机构的位置例如阀门控制中，这种算法的输出对应的就是阀门开关的位置角度。所以我们称这种算法为”位置式PID”

B、增量式PID控制算法

图4.5增量式PID控制算法的简化示意图

    由位置式算法可以求出u(k)：

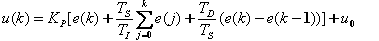
    我们接下来再求出u(k-1)

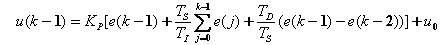
两式相减，得到控制量的增量算法：

代入并化简合并得：

从上式可以看出，上式已经看不出P、I、D左右的直接关系。我们只要储存最近的三个误差采样值e(k)、e(k-1)、e(k-2)就够了

五、改进的PID控制器

在实际的应用中，基本的PID控制器往往效果不够完美。我们需要使用改进型的PID控制器，下面将给大家介绍几种实用的PID控制器的变形。这里我们YJ团队常用的就是位置式PID控制器

A、PID输出饱和限幅

实际的系统中，存在着饱和特性。当输入量达到一定值之后，控制系统的输出将不再增长，系统进入饱和区。这就要求控制系统的输出必须在谋和范围之内，也就是：

Umin < U < Umax

在程序中，在最后输出时使用if-else判断即可实现上述的PID输出饱和限幅。代码如下：

图4.6 PID输出饱和限幅

B、积分饱和

在位置式PID中，”饱和”主要是由积分项过大引起的。这里我们称之为”积分饱和”，通常积分项不应该太大，我们应该限制其值。这里我们使用的是抗饱和积分法：

当我们的积分项大于最大的积分值的时候，我们的积分项只负责累加负的偏差值。而当我们的积分项小于最小的积分值的时候，我们的积分项只负责累加正的偏差值。从而实现抗饱和积分。

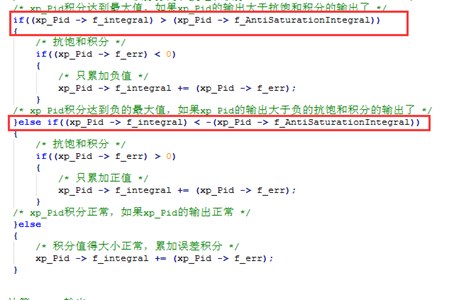
图4.7PID抗饱和积分

C、积分分离

在偏差较大的时候不进行积分作用，只有当偏差在一定的范围时才进行积分作用。这里我们采用的就是积分分离的方法。

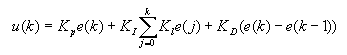
式中，我们K1就是计算的输出结果是否需要积分的标志位。

式中就是偏差的阈值。

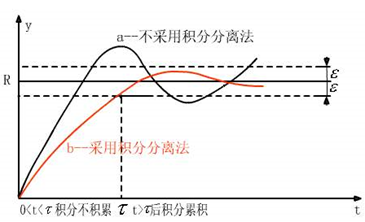
图4.8积分分离效果图

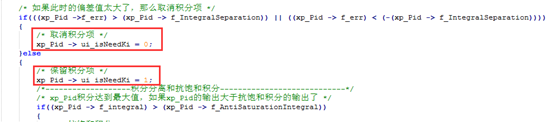
4.9积分分离c语言代码1

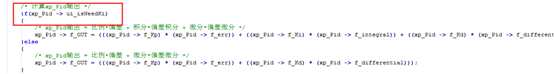
图4.10积分分离c语言代码2

六、PID的c语言实现

这里我建议大家根据位置式离散化的PID公式读一下下面的代码，很简单的。

头文件如下：

七、PID的各参数规律

这里以前我写过一篇博文不够完善，在这篇文章中我重新分析一遍。同时在我们文件夹中也提供了一个PID算法模拟软件，大家可以玩一下。原博客链接在这里：

http://blog.csdn.net/zzw5945/article/details/53998859

这里先推荐大家看一个PID参数整定的gif，很形象生动大家一定要看。链接如下：

https://en.wikipedia.org/wiki/PID_controller#/media/File:PID_Compensation_Animated.gif

A、Kp比例系数对系统响应的影响：

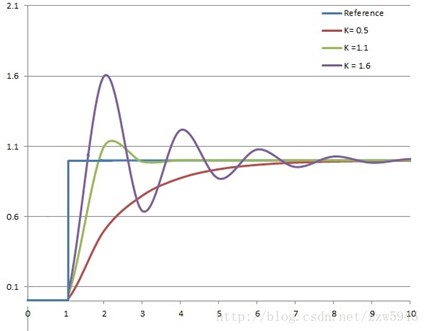
图 7.1 分析Kp参数对系统响应的影响

如图：当Ki,Kd保持为常量时，改变Kp。图上在t = 1s时，给系统一个阶跃信号，然后调节Kp比例项的值。图中红线为Kp = 0.5时候的响应曲线，绿线为Kp = 1.1时候的响应曲线，紫线为Kp = 1.6时的响应曲线。（注：我认为上图有问题，纯比例Kp环节我认为是存在静差的。所以上图稳定的时候 应该和期望值之间有一定的稳态误差，如下图7.2所示。但是我没找到合适的图所以就用这个了）

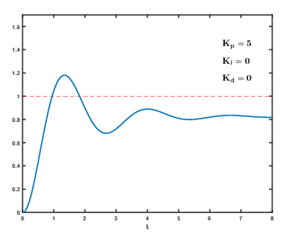
图7.2 纯比例环节系统输出响应曲线

从图7.1进行分析，可以得到以下信息：

红线：

当Kp比例项较小时，响应无超调无震荡，上升时间较长，但是稳定时间很长，延时时间长。

绿线：

当Kp比例项增大时，响应有较小超调，上升时间明显缩短，稳定时间缩短。

紫线：

当Kp比例项足够大时，响应曲线超调较大，震荡很多次，上升时间继续缩短，但是稳定时间却增长了。

如果继续增大Kp值呢？？这里图上没有反应，但是我们可以推测一下：上升时间继续减小，超调继续增大，震荡次数增大，最终系统失控发散，系统性能恶化。所以调PID参数时一定要小心，Kp值不能过大。总结以下：Kp在一定范围内可以调节系统的快速性，但是会影响系统的稳定性，Kp也会影响到系统的准确性。

B、Ki积分系数对系统响应的影响：

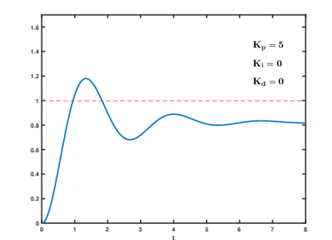
图7.3 Kp = 5 Ki = 0时系统输出响应

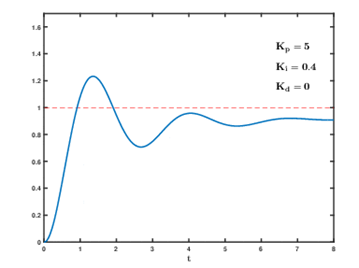
图7.4 Kp = 5 Ki = 0.4时的系统输出响应

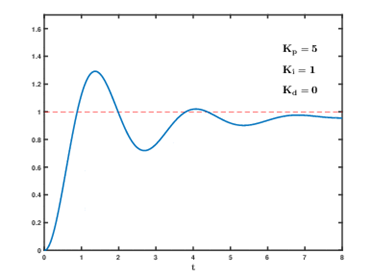
图7.5 Kp = 5 Ki = 1.0时的系统输出响应

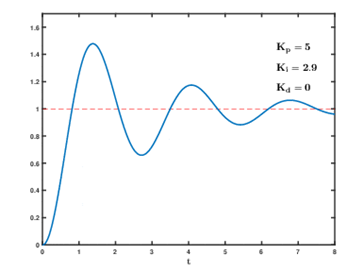
图7.6 Kp = 5 Ki = 2.9时的系统输出响应

    从图7.3、7.4、7.5、7.6这四幅图中，我们能从图上可以看出Ki是用来消除静差的。静差其实就是我们名词解释中的稳态误差。我们这里几幅图都使用的是控制变量法，控制Kp一致然后在不同的Ki参数下观察曲线的变化规律。我们可以看出在一定范围内，Ki增大将减小稳态误差（静差），但是从上面几幅图中我们也能看出Ki其实和Kp的作用类似，属于”+”作用，ki虽然在能减小静差，但是系统也会不稳定。总结一下ki的作用如下：

    Ki在一定范围内调节能减小系统静差，增加系统的快速性，但是会降低系统的稳定性。当Ki过大时会引起系统的不稳定。

C、Kd微分系数对系统响应的影响：

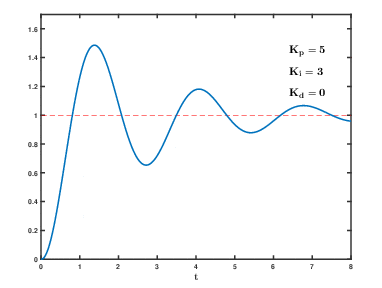
图7.7 Kp Ki为定值，kd = 0时的系统输出响应

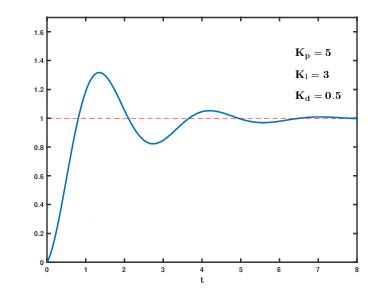
图7.8 Kp Ki为定值，kd = 0.5时的系统输出响应

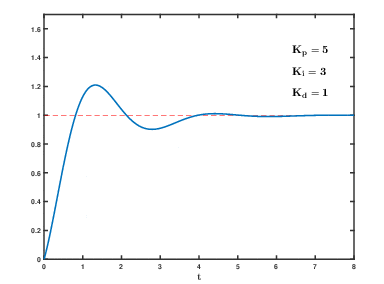
图7.9 Kp Ki为定值，kd = 1.0时的系统输出响应

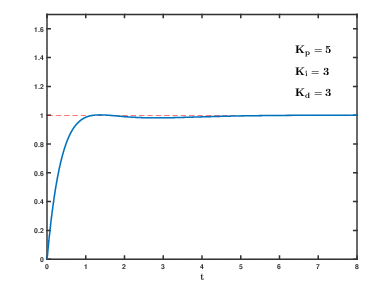
图7.10 Kp Ki为定值，kd = 3.0时的系统输出响应

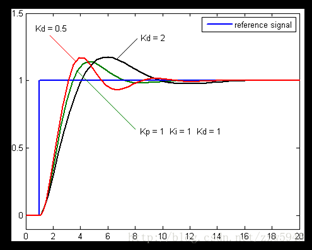
图7.11 Kd对系统输出响应影响

Kd的作用总结：Kd可以理解成阻尼系数。也就是在一定程度上可以抑制超调，减小超调量。但是能增强系统的稳定性，但是会稍微延长一定的上升时间也就是说会影响一点快速性。

八、四轴与自平衡小车PID参数整定调试台

A.微型四轴PID调试设备

需要大家购买：6*6mm内径万向节*1如图8.1所示、M3*10mm铜柱*2个（外径是4.7mm），2020型材或者碳杆。要求2020型材中间的孔径能插入一个4.7mm外径的M3铜柱。这里型材至少买一根，如果买的多的话还应该买点2020型材角件进行固定，然后可以搭出一个底座架如图8.4所示。这里我们买的万向节是二维运动的，我们在做我们的微型四轴PID调试台的时候，调PID应该是单轴运动的。所以我们要通过铜柱将万向节的其中一个轴固定住，只让它一个轴运动（让铜柱抵住万向节，就能实现）如下图8.5所示，连接四轴和万向节使用的就是铜柱和螺母，连接万向节和型材使用的也是铜柱。

我们这中调试台是为了微型四轴的调试而搭建的，如果是其他大型的四轴可能不能适用。得想其他办法

图8.1万向节

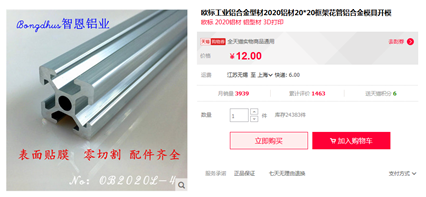
图8.2型材

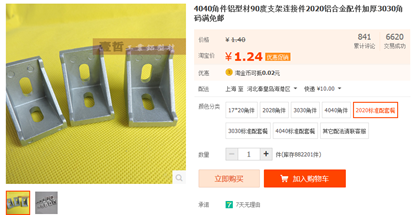
图8.3 2020角件型材铝

图8.4型材架

图8.5微型四轴PID调试架示意图

B.Qav250穿越机PID调试设备

这里我们的QAV250算是小型无人机，但是用上面那种调试设备就不是特别适合了。这里我们使用的是如下图所示的调试架，我们买了一个丝杠，然后将四轴绑在丝杠上进行调试的。

图8.6 QAV250穿越机PID调试架示意图

C.自平衡小车PID调试设备

自平衡小车的调试最简单方便，不需要购买任何配件。调试的时候我们直接用腿直接夹住自平衡小车的车轮，让车的上部分运动就可以进行PID调试了。

九、单级PID参数整定经验

单级PID由于效果不如串级PID完美，我们以前使用过单级PID。但是自从串级PID玩习惯了之后一直都在用串级PID，所以我们讲解的重点是串级pid的调试方法。关于单级PID的整定经验，我这里简单给大家讲讲：（单级PID没有留下调试图片，所以不是特别好描述）。

    调试PID时，我们需要使用电脑串口上位机显示出实际值曲线和目标给定值曲线。这里我们使用的上位机是YJ_Chart YJ串口上位机，单片机的串口与电脑YJ_Chart上位机通信的接口程序详见我们的debug.c文件。或者大家打开我们提供的四轴驱动工程代码，找到debug驱动工程即可进行学习了解。更多资料请访问我们的网站——www.yanjuntech.cn下载了解。

    先总结一下我们的PID参数整定方法：

1. 如果只需要调节一个环的PID，也就是所谓的单级PID，我们直接使用下面这几点经验即可。如果是串级PID我们需要先调试内环，再调试外环。
   
2. 首先我们通过写程序以及搭硬件调试设备，先单独的调试一个轴的PID参数
   
3. 调节PID参数之前，我们需要明确我们的PID结构，需要明确输入量期望值，实际值的物理意义。比如四轴单级PID，输入量就是遥控器给定的目标角度，实际值就是通过姿态传感器解算出来的姿态角度。
   
4. 调试PID参数之前，最最重要的就是一定要确定反馈回来的数据是正确的，如果反馈值不正确，再怎么调试PID参数都是徒劳的。所以调试之前一定要确定反馈量正确。
   
5. 调节PID参数的时候，我们需要看 具体现象以及 实际值与目标期望值的曲线。（使用串口上位机，将数据发送到电脑上位机上打印曲线）
   
6. 在调试Kp Ki Kd的时候，第一步要做的就是要确定好Kp Ki Kd参数的”+-“必须先确定正负，然后再开始调节PID参数。我们常用2种方法分析”+-“号，一种是理性分析法，一种是经验调试法。
   
7. 理性分析法，比如四轴，总共4个电机，顺时针方向分别为1.2.3.4，也就是23和14在x轴方向上，12和34在y轴方向上。先假设四轴只单方向运动，假设按x轴方向运动，也就是向23或者14边运动。假设向23边偏此时实际的x轴角度数据为+23度，目标值是0度，那么偏差就是-23度。飞行器想稳定到0度，也就是23边的电机需要转动快一点，14边要慢一点。由比例环节就是kp*偏差，那么这时候就能根据这一点和最后的控制量输出来确定Kp的”+-“号。另一种方法就是 参数经验法了，直接控制其他两个系数为0，然后设置一个比较大一点的大概合理的值然后根据实际现象确定正负号。
   
8. 单轴PID参数先从Kp进行调节，调节方法是1-2-4-8-16……先二倍法，然后使用二分法调节。观察现象如果发现Kp大了就减小一半，然后再在新的范围内调节。
   
9. Kp调试完成后再考虑是否调节Ki，是否需要消除静差。
   
10. 微型四轴单级姿态环PID调试经验
    

这里我们仅仅给大家介绍姿态环PID的调试经验，可能有的还需要高度环和位置环PID。我们在讲解的时候仅给大家讲解姿态环PID。

首先，我们微型四轴单级PID控制框图，了解一下基本的控制原理。这里输入的是期望角度，这个在实际应用中对应的是遥控器给定的目标角度（遥控器遥杆给定的值）。而反馈通道反馈回来的就是实际的姿态角度。然后目标角度和实际角度就存在偏差，偏差送入PID调节器进行调节，调节输出量作用在PWM电机上，电机的转速不同又间接影响到我们四轴的飞行姿态从而实现单级的闭环控制。

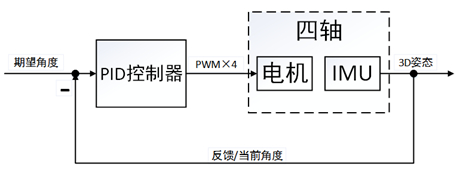
图9.1 微型四轴的单级PID框图

1. 在调试PID参数之前，我们应该把要用到的程序都要搞好，同时确定好反馈量确实正确。也就是说已经做好了调试PID参数的所有准备工作。（再说一句：调试PID参数之前一定要确定好反馈量一定是正确的，这个很重要很重要）。
   
2. 将微型四轴固定在我们准备好的硬件调试台上（只能绕一个轴运动，我们调试PID的时候都是一个轴一个轴调试-分轴调试），然后连接上jlink下载器和USB转串口线，打开YJ_Chart（我们将YJ_Chart也完全开源了）用于显示实际值和期望值曲线。在调试的过程中可以参考。
   
3. 写好调试程序，可以将实际值和目标期望值打印到电脑上位机上这样我们就能定性的观看参数调试的效果曲线了。同时我们应该写好相应的基础程序，包括PID运算相关的程序。
   
4. 我们要修改程序，调试四轴PID的时候，我们调试经验是一个轴一个轴的调试，所以我们需要注释掉其他轴代码，或者在最后的输出的时候，不加上其他轴的PID输出如下：
   

图9.2 单轴PID代码片段

    上面这个+-号实际是根据四轴的空气动力学来确定的，关于四轴中的空气动力学请见本文的第11部分。

    整定四轴的姿态环PID，实际上整定的就是三轴姿态角的PID——俯仰角、横滚角、偏航角。整定时正如我们上面说的修改程序固定到调试架上用串口打印曲线，然后一个轴一个轴的调试。

单级PID参数整定举例——x轴参数整定

    下面我拿x轴举例子，来进行PID调试。

    我们的实际值其实就是遥控器给定的值，也就是所谓的期望值x_AttitudeTargetData.f_X（也要写相应的程序，用来获取遥控器的设定值）。而我们的实际值其实就是我们四轴的实际姿态x_AttitudeNow.x_AngleNow.f_X。计算PID运算伪代码就如下：

    本次偏差 = 目标值 – 实际值;

    本次微分 = 本次偏差 – 上次偏差;

    上次偏差 = 本次偏差;

    PID计算()函数，传入上述参数;

图9.3PID参数结构体

    如图9.3所示，红框中的参数都是我们都是能进行手动设定的。最上面三个参数分别是Kp、Ki、Kd——比例积分微分系数。如果我们需要使用积分分离功能，则还要设置积分分离阈值同时也应该设置抗饱和积分阈值。最后的PID输出，我们应该设置好PID的输出阈值。

    微型四轴的单级PID调试经验如下所示：

图9.4微型四轴调试设备

1. 调试之前，一定要确定反馈值（实际值）是正确无误的。如果反馈信号有问题，根本就调不出来参数。
   
2. 修改好程序，打开串口调试曲线软件。（单级的我没留调试过程中的图片，单级就简单口头说说，大家去看下面我写的串级的PID参数整定经验，那篇比较全）
   
3. 目标值由遥控器设定的值，实际值是四轴的实际姿态角，修改Kp，使用2倍2分法。先确定好Kp的”+-“号。然后按1-2-4-8-16-32-64…这样二倍法调试，然后比如64的时候参数效果有点小，但是改成128的时候，发现效果有点过头了。那么我们需要使用二分法进行调试，找64和128的中间值：96然后再64-96内调试确定如果小了，在96-128中间进行二分法调试。
   
4. Kp调试效果简述：四轴调试角度应该是-30度–+30度范围内，如果角度比较大的时候，受到重力的影响比较大，参数整定就不准确效果不好了。我们把四轴放到-20度方向，然后改Kp参数，当Kp比较小的时候四轴表现的效果是软趴趴，到不了目标值0。当Kp比较大的时候，也就是快速超过目标值，停不下来。当参数比较合适的时候会在中心位置震荡（0度附近运动）。
   
5. 大概能在目标值附近停住或者震荡，此时我们稍微再加Kd微分系数（也要确定好±），注意Kd效果是阻尼的效果，实际四轴效果是：当只有Kd比较大的时候，向x轴正方向运动假如4个电机顺时针分别是1.2.3.4号电机。假如向23电机方向快速运动，那么Kd正确的效果应该是 使电机的2.3号电机转动。以此确定Kd的方向。然后开始调试Kd的值，如果微分项没有除以采样时间（我们用的是0.002s采样时间），那么Kd值就比较大可能上百上千。如果微分项除以了采样时间，那么Kd值就比较小了。不加Kd，只有合适的Kp能在平衡位置震荡。而加上Kd之后，效果就很好了，能比较稳定了。
   
6. 大家在上面的调试过程中，将目标值曲线和实际值曲线打印出来。来看看PID的整定规律。看曲线看看稳定后的实际值和目标值之间的静差（稳态误差）是否比较大。如果比较大，可能就需要加Ki参数，来调试。Ki调试过程实际看的是，稳定后的目标值与实际值之间静差的大小。把曲线打印出来，就能很好的观察调试参数。
   

好了关于单级PID整定方法，我们就讲简单分享到这里。没有留下太多图片可能大家不是特别好理解，下面的串级PID参数整定，我留下的图片比较多，大家去看看串级PID参数的整定，相信你会有很大收获的。

1. 自平衡小车单级PID调试经验
   

   自平衡小车的单级PID和微型四轴的单级PID参数调试经验差不多，这里不过多介绍了。自平衡小车的姿态环单级PID（自立PID） 目标值一般情况下都是0度，实际值就是小车的实际角度。
   

   
   

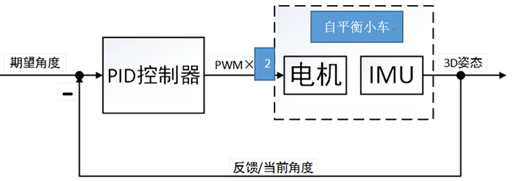
图9.2 自平衡小车的单级PID框图

调试PID时，我们需要使用电脑串口上位机显示出实际值曲线和目标给定值曲线。这里我们使用的上位机是YJ_Chart YJ串口上位机，单片机的串口与电脑YJ_Chart上位机通信的接口程序详见我们的debug.c文件。或者大家打开我们提供的四轴驱动工程代码，找到debug驱动工程即可进行学习了解。更多资料请访问我们的网站——www.yanjuntech.cn下载了解

    建议大家先读一下单级PID上面总结的一些实用经验。

1. 自平衡小车串级PID调试经验
   

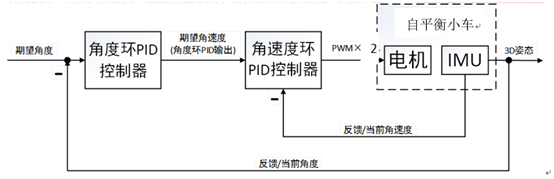
图10.1 自平衡小车串级PID框架

    首先我们已经写好了所有基础程序，做好了准备工作。这里自平衡小车的PID整定过程中的效果曲线我记录的比较完整，所以这部分可以比较清晰的看明白。如图10.1所示，自平衡小车的姿态环串级PID有两个闭环，分别是内环——角速度环、外环角度环。我们在整定的时候是先整定内环角速度环，整定好了之后再来整定外环角度环的。

    当然如果想实现自平衡小车稳定自立以及前进和拐弯的话，除了姿态环PID还需要速度环和转向环PID。这里我们为了省事，就拿姿态环的PID参数整定过程给大家讲解PID参数的整定经验。

图10.2两轮自平衡小车实物图

    我们插上USB线（板子上已经集成USB转串口芯片了），修改程序准备开调PID参数。我们调试的时候是先调内环也就是角速度环的PID参数，调试好后再调外环的PID参数。

1. 角速度内环整定经验
   

首先改代码，改成内环调试用的代码。如下图10.3所示，内环调试时PID的内环给定设置成遥控器的给定值，也就是遥控器的给定设置成目标角速度。而实际值就是我们自平衡小车的实际运动角速度（陀螺仪测量出来的经过低通滤波的角速度）。

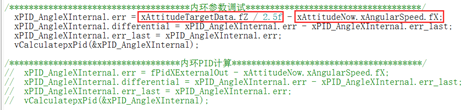
图10.3角速度内环参数调试

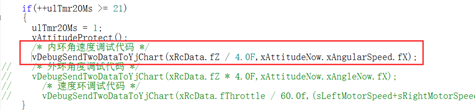
图10.4角速度环发送到上位机

    图10.4就是我们将目标角速度（遥控器设定的值）和实际角速度发送到电脑上位机上用曲线显示出来便于我们调试用。见下图10.5所示：

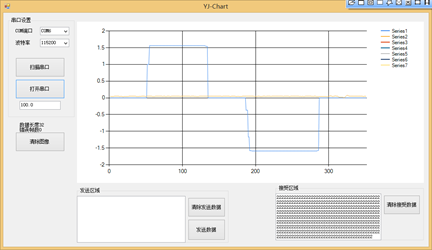
图10.5遥控器给定值曲线-蓝线

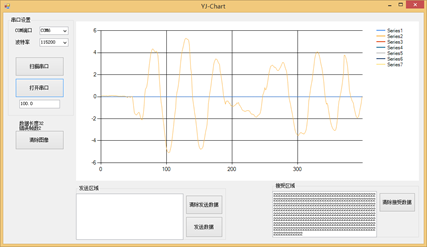
图10.6小车实际角速度-黄线

    如上图10.5和10.6所示，蓝线为遥控器控制的值也就是我们所说的目标值。黄线为平衡小车的实际角速度值打印出来的曲线也就是我们所说的实际值。看10.6，我们遥控器没有设置给定值，目标期望也就为0弧度/s，实际值是我们晃动小车，小车打印出来的实际角速度值。下面我们用腿夹住平衡小车的两个轮子，我们要开始调试平衡小车的内环角速度环的PID参数了如图10.7所示：

图10.7用腿夹住小车两轮

    我们下面开始调PID参数，先调Kp确定好Kp的符号，其他值保持为0：

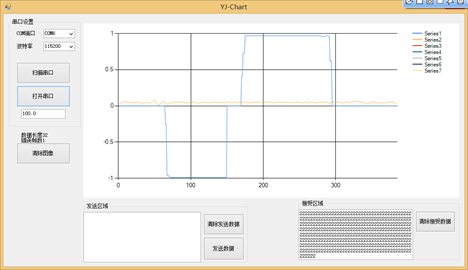
图10.8Kp = 10实际值与目标值曲线

    当Kp = 10，太小了，改变目标期望值的时候，实际的角速度并没有变化，所以是Kp太小，效果太软。我们继续加Kp = 20；二倍法，如下图10.9所示：发现Kp = 20时，改变目标角速度，但是实际的角速度也并没有任何变化。所以值还是小，我们继续增大Kp 的值。继续使用二倍法，增加到Kp = 40；

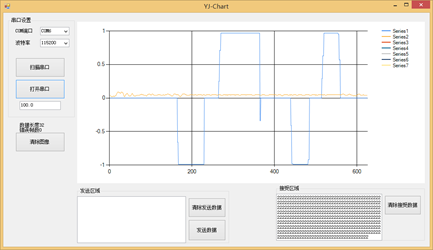
图10.9 Kp = 20内环角速度调试

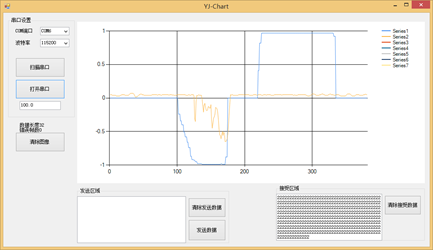
图10.9 Kp = 40内环角速度调试

    我们可以看到Kp = 40，有效果了，但是力量依然不够还是小我们继续加大Kp = 80：

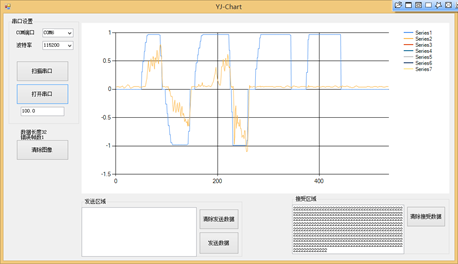
图10.9 Kp = 80内环角速度调试

    从图上我们可以看出，Kp = 80时还是有点小。我们继续增大一倍到160：

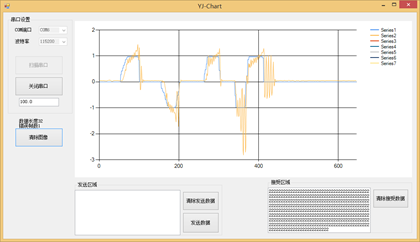
图10.9 Kp = 160内环角速度调试

    感觉效果有点过头，有点大了我们需要使用二分法砍到120然后看看效果。不够我们先继续增大到320，看看Kp过大是什么效果：

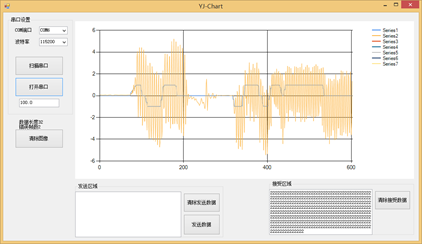
图10.9 Kp = 320内环角速度调试

    可以看到，Kp = 320时。系统已经很不稳定了崩溃了……，我们将Kp改小然后调试，我们发现的不错的效果值是Kp = 130。然后让我们加一点Kd，看看实际效果

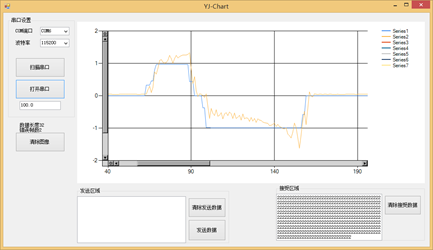
图10.10 Kp = 130 Kd = 500内环角速度调试

    当然大家如果再好好调调参数，效果比这个还好还是有可能的毕竟我们这里只是粗略的调试，到这个程度实际的效果就是用遥控器控制平衡小车，小车能按遥控器设置的角速度运动，我们可以通过遥控器控制小车停在竖直位置。下

    到这个程度，就说明我们的内环就已经调试完毕了，下面我们要开始调试外环的角度环PID参数。

1. 角度外环参数整定经验
   

   首先也是改程序，改成外环角度环调试的代码。

   
   

图10.11 角度外环调试代码

发送目标角度和实际角度数据到上位机。然后下面我们要开始调试了：

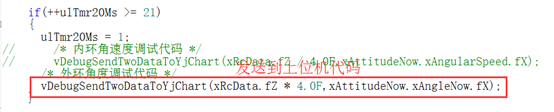
图10.12 角度发送到上位机代码

    首先要确定是外环的Kp系数的符号，外环一般只需要Kp比例系数就可以了。Kp可以增加系统的快速性，合适的外环Kp参数可以快速稳定到目标角度。一般外环的Kp比较小，内环的Kp比较大（系统有关和程序写的方式有关），大家可以使用PID的输出除以大概的偏差大致的得到PID的Kp参数的数量级。比如PID输出量是300，而偏差大概是3左右，那么Kp的数量级就是100左右（内环的数量级），而外环数量街：PID的输出量是2.0左右，偏差为20度的话，则kp的范围大致为0.1左右，所以在调试PID的时候可以首先通过简单计算确定出参数的大致范围。

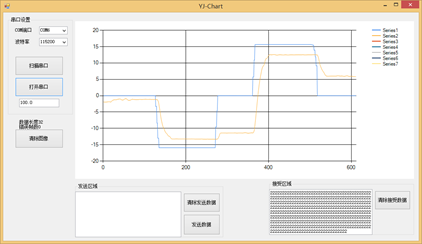
图10.13 角度外环Kp = 0.1时的目标角度和实际角度

    由图可以看出，参数有点小，实际值追不上目标值的变化。

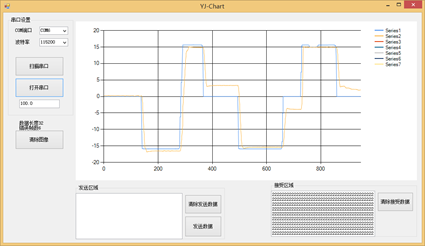
图10.14 角度外环Kp = 0.2时的目标角度和实际角度

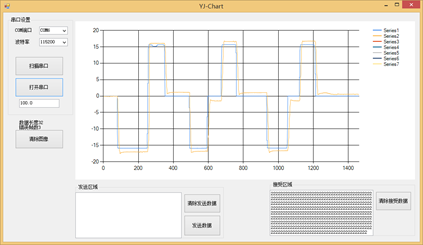
图10.15 角度外环Kp = 0.3时的目标角度和实际角度

    由图可以看出，Kp = 0.3的时候效果很好，快速性很高响应速度很快。跟随给定的效果很好，而且没有太多超调。效果很好，于是姿态环外环角度环的PID参数就调试出来了。当外环角度环Kp过大的时候，效果如下图所示10.16：

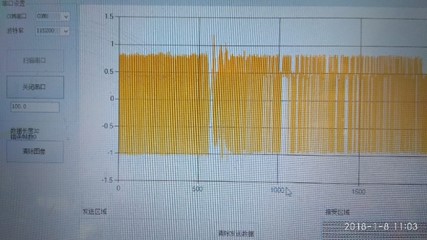
图10.16外环Kp比较大系统崩溃

    效果视频如下链接所示：

    总结一下：有的串级PID的参数整定还是比较容易的，借用串口显示曲线的软件将比较方便的的调试我们的PID参数。

1. 先调试内环，再调试外环
   
2. 修改程序，使用串口助手打印曲线
   
3. 自平衡小车电机控制内环使用PD，外环使用P就能实现很好效果
   
4. 调试PID参数的时候先调试P参数再调试D参数最后根据效果调试I参数
   

B、微型四轴串级PID调试经验

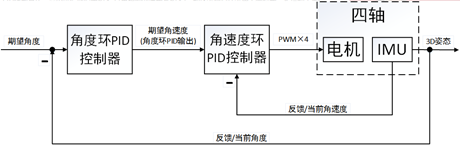
图10.17四轴串级PID框架

四轴的串级PID参数调试，过程和上面差不多。只不过四轴的姿态是3个姿态角，而自平衡小车的姿态角只有1个。但是我们在调试的时候，实际上也是使用调试架控制四轴只能绕一个轴运动。

图10.18单轴PID调试架

    然后我们先调试x轴的PID参数，y轴参数和x轴差不多可以直接复制。调试步骤也是先调P再调D最后调I。

1. 四轴中的空气动力学
   

微型四轴飞行器有四个电机，如何才能通过控制四个电机的转速来实现，最终的控制三个轴的姿态角呢？

这就是空气动力学需要解决的问题。

先给出四轴的示意图

图2-1 四轴飞行器示意图

为方便说明，我们把电机进行编号，顺时针方向分别是1.2.3.4号电机

飞行器保持悬停， 4 个电机的转速保持一致，来使飞行器保持水平。

四个电机的转速=悬停油门。

当我们希望飞行器向右飞的时候，我们设定在第一种情况的基础上，增加左边两个电机（ 1,4）的转速，减小右边两个电机（ 2,3）的转速。

1 号电机= 悬停油门 + 右倾的量。

4 号电机 = 悬停油门 + 右倾的量。

2 号电机= 悬停油门 ‐ 右倾的量。

3 号电机=悬停油门 ‐ 右倾的量。

当我们希望飞行器向左飞的时候，上面的公式依然成立，只不过右倾的量是负数了。

当我们希望飞行器向前飞的时候，那么我们要增加后面一组电机（ 3,4）的转速，减小前面一组电机（ 1,2）的转速。

1 号电机= 悬停油门 ‐ 前飞的量。

2 号电机= 悬停油门 ‐ 前飞的量。

3 号电机=悬停油门 + 前飞的量。

4 号电机 = 悬停油门 + 前飞的量。

飞行器向后飞的情况，上面公式依然成立，前飞的量为负数。

当我们希望飞行器顺时针旋转， 我们增加 2 号， 4 号 对角线两个电机的转速，减小 1号， 3 号这条对角线电机的转速。（力的方向应该是右手螺旋法则）

3 号电机=悬停油门 ‐ 旋转的量。

2 号电机= 悬停油门 + 旋转的量。

4 号电机 = 悬停油门 + 旋转的量。

1 号电机= 悬停油门 ‐ 旋转的量。

当我们希望飞行器逆时针旋转， 我们减小 2 号， 4 号对角线两个电机的转速，增加 1号， 3 号这条对角线电机的转速。继续使用上面的公式。

最后，针对一个电机，它同时要负责前后左右和旋转的情况， 那它就叠加了 4 种情况下的值：

1 号电机 = 悬停油门 + 右倾的量 ‐ 前飞的量 ‐ 旋转的量

2 号电机 = 悬停油门 ‐ 右倾的量 ‐ 前飞的量 + 旋转的量

3 号电机 = 悬停油门 ‐ 右倾的量 + 前飞的量 ‐ 旋转的量

4 号电机 = 悬停油门 + 右倾的量 + 前飞的量 + 旋转的量

下图程序中规定的电机顺序和上述不同，所以不一样。程序表达大概就是下面这个意思。

转载请注明：燕骏博客 » PID控制器算法原理讲解从入门到精通详细教程工控PID算法参数整定串级PID算法讲解